motivação

Ser blogueiro… 
É dedicar tempo, conciliar atividades, administrar ideias.
É lidar com todas as emoções. E, a todo tempo, estar preparado para compartilhá-las.
É ter pique para curtir um evento e mesmo ao cansaço, reunir material, referências e editar fotos para trazer a notícia aos leitores.
É atualizar-se, ser útil enquanto veículo de informação.
É formar opiniões, lidar com as diferenças e sobretudo, respeitá-las.
É ajudar, tirar dúvidas, aflições, acalmar a alma. 
É transformar choro em poesia, política em debate, passarela em moda de rua. 
É buscar inspiração num sábado de sol, ou tarde de segunda-feira chuvosa.
Não importa o tempo, a moda ou estação. Ser blogueiro é amar. 
É amor pela escrita. Amor que transcende ideias, coleciona sonhos e abre as portas.

Geometria Plana - Aula 3 - Triângulos - Prof. Gui

Geometria Plana - Aula 2 - Polígonos - Prof. Gui

Geometria Plana - Aula 1 - Ângulos - Prof. Gui

Bem Vindo ao Blog!!

A partir de agora você já pode visitar essa sessão do nosso blog, onde sempre encontrará comentários, notícias e novidades interessantes sobre a matemática, bem como as etapas e conquistas alcançadas pelo professor Rodrigo Penha.

Entre e fique a vontade para já começar comentando o que achou do nosso blog.

Um forte abraço. 

Rodrigo Penha.

A Esfera na Geometria Espacial

A Esfera é uma figura simétrica tridimensional que faz parte dos estudos de geometria espacial. Em outras palavras, a esfera é um sólido geométrico obtido através da revolução da semicircunferência sobre um eixo, composto por uma superfície fechada na medida que todos os pontos estão equidistantes do centro (O). Alguns exemplos de esfera são o planeta, uma laranja, uma melancia, uma bola de futebol, dentre outros.

Componentes da Esfera

• Superfície Esférica: corresponde ao conjunto de pontos do espaço no qual a distância do centro (O) é equivalente ao raio (R).
• Cunha Esférica: corresponde à parte da esfera obtida ao girar um semicírculo em torno de seu eixo.
• Fuso Esférico: corresponde à parte da superfície esférica que se obtém ao girar uma semicircunferência de um ângulo em torno de seu eixo.
• Calota Esférica: corresponde a parte da esfera (semiesfera) cortada por um plano.

Para compreender melhor os componentes da esfera, analise as figuras abaixo:

 

Fórmulas da Esfera

Veja abaixo as fórmulas para calcular a área e o volume de uma esfera:

Área da Esfera

Para calcular a área da superfície esférica, utiliza-se a fórmula:

Ae = 4.п.r2

Donde:

Ae= área da esfera

П (Pi): 3,14

r: raio

Volume da Esfera

Para calcular o volume da esfera, utiliza-se a fórmula:

Ve = 4/3п.r​3

Donde:

Ve: volume da esfera

П (Pi): 3,14

r: raio

Conheça também outras figuras geométricas espaciais: Geometria Espacial.

Exercícios Resolvidos

1. Qual a área da esfera de raio √3 m?

Para calcular a área da superfície esférica, utiliza-se a expressão:

Ae=4.п.r2

Ae = 4. п. (√3)2

Ae = 12п

Logo, a área da esfera de raio √3 m, é de 12 п.

2. Qual o volume da esfera de raio ³√3 cm?

Para calcular o volume da esfera, utiliza-se a expressão:

Ve = 4/3.п.r3

Ve = 4/3.п.(³√3)3

Ve = 4п.cm3

Portanto, o volume da esfera de raio ³√3 cm é de 4п.cm3.

Figuras Geométricas Espaciais

Segue abaixo algumas das figuras geométricas espaciais mais conhecidas:

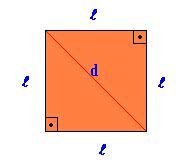
Cubo

O cubo é um hexaedro regular composto de 6 faces quadrangulares, 12 arestas e 8 vértices sendo:

Área lateral: 4a2
Área total: 6a​2
Volume: a.a.a = a3

Dodecaedro

O Dodecaedro é um poliedro regular composto de 12 faces pentagonais, 30 arestas e 20 vértices sendo:

Área Total: 3√25+10√5a2
Volume: 1/4 (15+7√5) a3

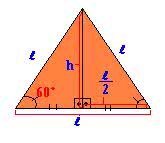
Tetraedro

O Tetraedro é um poliedro regular composto de 4 faces triangulares, 6 arestas e 4 vértices sendo:

Área total: 4a2√3/4
Volume: 1/3 Ab.h

Octaedro

O Octaedro é um poliedro regular de 8 faces formada por triângulos equiláteros, 12 arestas e 6 vértices sendo:

Área total: 2a2√3
Volume: 1/3 a3√2

Icosaedro

O Icosaedro é um poliedro convexo composto de 20 faces triangulares, 30 arestas e 12 vértices sendo:

Área total: 5√3a2
Volume: 5/12 (3+√5) a3

Prisma

O Prisma é um poliedro composto de duas faces paralelas que formam a base, que por sua vez, podem ser triangular, quadrangular, pentagonal, hexagonal. Além das faces o prima é composto de altura, lados, vértices e arestas unidos por paralelogramos. De acordo com sua inclinação, os prismas podem ser retos, aqueles em que a aresta e a base fazem um ângulo de 90º ou os oblíquos compostos de ângulos diferentes de 90º.

Área da Face: a.h
Área Lateral: 6.a.h
Área da base: 3.a3√3/2
Volume: Ab.h

Onde:
Ab: Área da base
h: altura

Pirâmide

A pirâmide é um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular, paralelogramo), um vértice (vértice da pirâmide) que une todas as faces laterais triangulares. Sua altura corresponde a distância entre o vértice e sua base. Quanto à sua inclinação podem ser classificadas em retas (ângulo de 90º) ou oblíquas (ângulos diferentes de 90º).

Área total: Al + Ab
Volume: 1/3 Ab.h

Onde:

Al: Área lateral
Ab: Área da base
h: altura

Curiosidades

• A palavra "geometria" vem do grego e corresponde a união dos termos "geo" de terra e "metria" de medida, que significa "medir terra."
• Os cálculos mais comuns em Geometria espacial são para determinar o comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas.
• Outras figuras geométricas espaciais: cilindro, cone, esfera.
• Os "Sólidos Platônicos" são poliedros convexos conhecidos desde a antiguidade clássica. Os cinco "sólidos platônicos" são: tetraedro, cubo, octaedro, dodecaedro, icosaedro.

Entenda mais sobre os Sólidos Platônicos no vídeo: Sólidos de Platão

Geometria Espacial

A Geometria Espacial corresponde a área da matemática que se encarrega de estudar as figuras no espaço, ou seja, aquelas que possuem mais de duas dimensões.

De modo geral, a Geometria Espacial pode ser definida como o estudo da geometria no espaço. Assim, tal qual a Geometria Plana, ela está pautada nos conceitos basilares e intuitivos que chamamos “conceitos primitivos” os quais possuem origem na Grécia Antiga e na Mesopotâmia (cerca de 1000 anos a.C.).

Não obstante, Pitágoras e Platão associavam o estudo da Geometria Espacial ao estudo da Metafísica e da religião; contudo, foi Euclides a se consagrar com sua obra “Elementos”, onde sintetizou os conhecimentos acerca do tema até os seus dias.

Entretanto, os estudos de Geometria Espacial permaneceram estanques até o fim da Idade Média, quando Leonardo Fibonacci (1170-1240) escreve a “Practica Geometriae” e, séculos depois, Joannes Kepler (1571-1630) rotula o “Steometria” (stereo: volume/metria: medida) o cálculo de volume, em 1615.

Para saber mais sobre a geometria, leia: Geometria Plana.

Características da Geometria Espacial

A Geometria Espacial estuda os objetos que possuem mais de uma dimensão e ocupam lugar no espaço. Por sua vez, esses objetos são conhecidos como "sólidos geométricos" ou "figuras geométricas espaciais". Conheça melhor alguns deles:

• prisma
• cubo
• paralelepípedo
• pirâmide
• cone
• cilindro
• esfera

Dessa forma, a geometria espacial é capaz de determinar, por meio de cálculos matemáticos, o volume destes mesmos objetos, ou seja, o espaço ocupado por eles.

Contudo, o estudo das estruturas das figuras espaciais e suas inter-relações é determinado por alguns conceitos básicos, a saber:

• Ponto: conceito fundamental a todos os subsequentes, uma vez que todos sejam, em última análise, formados por inúmeros pontos. Por sua vez, os pontos são infinitos e não possuem dimensão mensurável (adimensional). Portanto, sua única propriedade garantida é sua localização.
• Reta: composta por pontos, é infinita nos dois lados e determina a distância mais curta entre dois pontos determinados.
• Linha: possui algumas semelhanças com a reta, pois é igualmente infinita para cada lado, contudo, têm a propriedade de formar curvas e nós sobre si mesma.
• Plano: é outra estrutura infinita que se estende em todas as direções.

Geometria Plana

A geometria plana ou euclidiana é a parte da matemática que estuda as figuras que não possuem volume, tal qual as figuras que fazem parte da geometria espacial.

A geometria plana também é chamada de euclidiana, uma vez que seu nome representa uma homenagem ao geômetra Euclides de Alexandria, considerado o “pai da geometria”.

Curioso notar que o termo geometria é a união das palavras “geo” (terra) e “metria” (medida); assim, a palavra geometria significa a "medida de terra".

Conceitos de Geometria Plana

Alguns conceitos são de suma importância para o entendimento da geometria plana, a saber:

• Ponto: Conceitos adimensional, uma vez que não possuem dimensão. Os pontos determinam uma localização e são indicados com letras maiúsculas.
• Reta: a reta, representada por letra minúscula, é uma linha ilimitada unidimensional (possui o comprimento como dimensão) e pode se apresentar em três posições: horizontal, vertical ou inclinada. Dependendo da posição das retas, quando elas se cruzam, ou seja, possuem um ponto em comum, são chamadas de retas concorrentes; por outro lado, as que não possuem ponto em comum, são classificadas como paralelas.
• Segmento de Reta: Diferente da reta, o segmento de reta é limitado pois corresponde a parte entre dois pontos distintos. Não obstante, a semirreta é limitada somente num sentido, visto que possui início, e não possui fim.
• Plano: corresponde a uma superfície plana bidimensional, ou seja, possui duas dimensões: comprimento e largura. Nessa superfície que se formam as figuras geométricas.
• Ângulos: são formados pela união de dois segmentos de reta, a partir de um ponto comum, chamado de vértice do ângulo. São classificados em: ângulo reto (Â = 90º), ângulo agudo (0º < Â < 90º) e ângulo obtuso (90º < Â < 180º).
• Área: A área de uma figura geométrica expressa o tamanho de uma superfície de modo que quando maior a superfície da figura, maior será sua área.
• Perímetro: corresponde a soma de todos os lados de uma figura geométrica.

Figuras da Geometria Plana

• Triângulo: polígono (figura plana fechada) de três lados, o triângulo é uma figura geométrica plana formada por três segmentos de reta. Segundo a forma dos triângulos, eles são classificados em: equilátero (possui todos os lados e ângulos internos iguais (60°); isósceles (possui dois lados e dois ângulos internos congruentes); e o escaleno (possui todos os lados e ângulos internos diferentes). No tocante aos ângulos que formam os triângulos, eles são classificados em triângulo retângulo (possui um ângulo de 90°); triângulo obtusângulo (possui dois ângulos agudos, ou seja, menor que 90° e um ângulo obtuso, maior que 90°); e o triângulo acutângulo (possui três ângulos de 90°).

• Quadrado: polígono de quatro lados iguais, o quadrado ou quadrilátero é uma figura geométrica plana que possuem os quatro ângulos congruentes: retos (90°).

• Retângulo: figura geométrica plana marcada por dois lados paralelos no sentido vertical e os outros dois paralelos, no horizontal. Assim, todos os lados do retângulo formam ângulos reto (90°).

• Círculo: figura geométrica plana caracterizada pelo conjunto de todos os pontos de um plano. O raio (r) do círculo corresponde a medida da distância entre o centro da figura até sua extremidade.

• Trapézio: Chamado de quadrilátero notável, pois a soma dos seus ângulos internos corresponde a 360º, o trapézio é uma figura geométrica plana que possui dois lados e bases paralelas, donde uma é maior e outra menor. São classificados em: trapézio retângulo (possui dois ângulos de 90º), trapézio isósceles ou simétrico (os lados não paralelos possuem a mesma medida), trapézio escaleno (todos os lados de medidas diferentes).

• Losango: quadrilátero equilátero, ou seja, formado por quatro lados iguais, o losango, junto com o quadrado e o retângulo, é considerado um paralelogramo, ou seja, um polígono de quatro lados, os quais possuem lados e ângulos opostos congruentes e paralelos.