Geometria Plana

A geometria plana ou euclidiana é a parte da matemática que estuda as figuras que não possuem volume, tal qual as figuras que fazem parte da geometria espacial.

A geometria plana também é chamada de euclidiana, uma vez que seu nome representa uma homenagem ao geômetra Euclides de Alexandria, considerado o “pai da geometria”.

Curioso notar que o termo geometria é a união das palavras “geo” (terra) e “metria” (medida); assim, a palavra geometria significa a "medida de terra".

Conceitos de Geometria Plana

Alguns conceitos são de suma importância para o entendimento da geometria plana, a saber:

• Ponto: Conceitos adimensional, uma vez que não possuem dimensão. Os pontos determinam uma localização e são indicados com letras maiúsculas.
• Reta: a reta, representada por letra minúscula, é uma linha ilimitada unidimensional (possui o comprimento como dimensão) e pode se apresentar em três posições: horizontal, vertical ou inclinada. Dependendo da posição das retas, quando elas se cruzam, ou seja, possuem um ponto em comum, são chamadas de retas concorrentes; por outro lado, as que não possuem ponto em comum, são classificadas como paralelas.
• Segmento de Reta: Diferente da reta, o segmento de reta é limitado pois corresponde a parte entre dois pontos distintos. Não obstante, a semirreta é limitada somente num sentido, visto que possui início, e não possui fim.
• Plano: corresponde a uma superfície plana bidimensional, ou seja, possui duas dimensões: comprimento e largura. Nessa superfície que se formam as figuras geométricas.
• Ângulos: são formados pela união de dois segmentos de reta, a partir de um ponto comum, chamado de vértice do ângulo. São classificados em: ângulo reto (Â = 90º), ângulo agudo (0º < Â < 90º) e ângulo obtuso (90º < Â < 180º).
• Área: A área de uma figura geométrica expressa o tamanho de uma superfície de modo que quando maior a superfície da figura, maior será sua área.
• Perímetro: corresponde a soma de todos os lados de uma figura geométrica.

Figuras da Geometria Plana

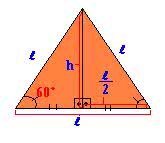
• Triângulo: polígono (figura plana fechada) de três lados, o triângulo é uma figura geométrica plana formada por três segmentos de reta. Segundo a forma dos triângulos, eles são classificados em: equilátero (possui todos os lados e ângulos internos iguais (60°); isósceles (possui dois lados e dois ângulos internos congruentes); e o escaleno (possui todos os lados e ângulos internos diferentes). No tocante aos ângulos que formam os triângulos, eles são classificados em triângulo retângulo (possui um ângulo de 90°); triângulo obtusângulo (possui dois ângulos agudos, ou seja, menor que 90° e um ângulo obtuso, maior que 90°); e o triângulo acutângulo (possui três ângulos de 90°).

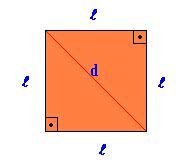
• Quadrado: polígono de quatro lados iguais, o quadrado ou quadrilátero é uma figura geométrica plana que possuem os quatro ângulos congruentes: retos (90°).

• Retângulo: figura geométrica plana marcada por dois lados paralelos no sentido vertical e os outros dois paralelos, no horizontal. Assim, todos os lados do retângulo formam ângulos reto (90°).

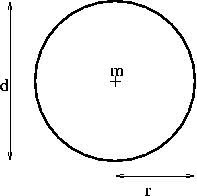
• Círculo: figura geométrica plana caracterizada pelo conjunto de todos os pontos de um plano. O raio (r) do círculo corresponde a medida da distância entre o centro da figura até sua extremidade.

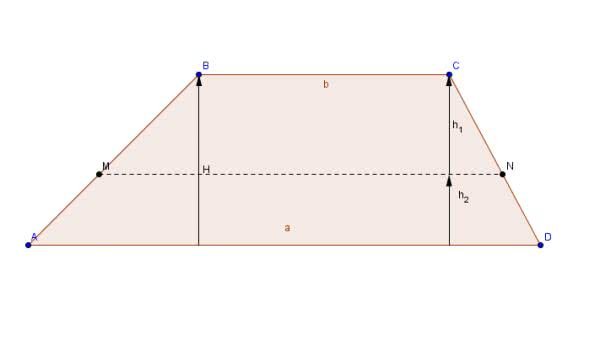
• Trapézio: Chamado de quadrilátero notável, pois a soma dos seus ângulos internos corresponde a 360º, o trapézio é uma figura geométrica plana que possui dois lados e bases paralelas, donde uma é maior e outra menor. São classificados em: trapézio retângulo (possui dois ângulos de 90º), trapézio isósceles ou simétrico (os lados não paralelos possuem a mesma medida), trapézio escaleno (todos os lados de medidas diferentes).

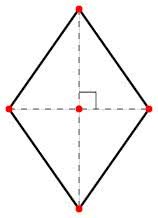
• Losango: quadrilátero equilátero, ou seja, formado por quatro lados iguais, o losango, junto com o quadrado e o retângulo, é considerado um paralelogramo, ou seja, um polígono de quatro lados, os quais possuem lados e ângulos opostos congruentes e paralelos.