A Esfera é uma figura simétrica tridimensional que faz parte dos estudos de geometria espacial. Em outras palavras, a esfera é um sólido geométrico obtido através da revolução da semicircunferência sobre um eixo, composto por uma superfície fechada na medida que todos os pontos estão equidistantes do centro (O). Alguns exemplos de esfera são o planeta, uma laranja, uma melancia, uma bola de futebol, dentre outros.

Componentes da Esfera

Superfície Esférica: corresponde ao conjunto de pontos do espaço no qual a distância do centro (O) é equivalente ao raio (R).
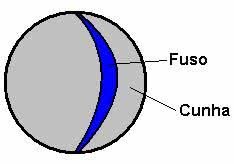
Cunha Esférica: corresponde à parte da esfera obtida ao girar um semicírculo em torno de seu eixo.
Fuso Esférico: corresponde à parte da superfície esférica que se obtém ao girar uma semicircunferência de um ângulo em torno de seu eixo.
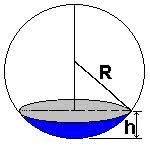
Calota Esférica: corresponde a parte da esfera (semiesfera) cortada por um plano.

Para compreender melhor os componentes da esfera, analise as figuras abaixo:

Veja abaixo as fórmulas para calcular a área e o volume de uma esfera:

Para calcular a área da superfície esférica, utiliza-se a fórmula:

Ae = 4.п.r2

Donde:

Ae= área da esfera

П (Pi): 3,14

r: raio

Para calcular o volume da esfera, utiliza-se a fórmula:

Ve = 4/3п.r3

Donde:

Ve: volume da esfera

П (Pi): 3,14

r: raio

Conheça também outras figuras geométricas espaciais: Geometria Espacial.

1. Qual a área da esfera de raio √3 m?

Para calcular a área da superfície esférica, utiliza-se a expressão:

Ae=4.п.r2

Ae = 4. п. (√3)2

Ae = 12п

Logo, a área da esfera de raio √3 m, é de 12 п.

2. Qual o volume da esfera de raio ³√3 cm?

Para calcular o volume da esfera, utiliza-se a expressão:

Ve = 4/3.п.r3

Ve = 4/3.п.(³√3)3

Ve = 4п.cm3

Portanto, o volume da esfera de raio ³√3 cm é de 4п.cm3.